Research

Summary

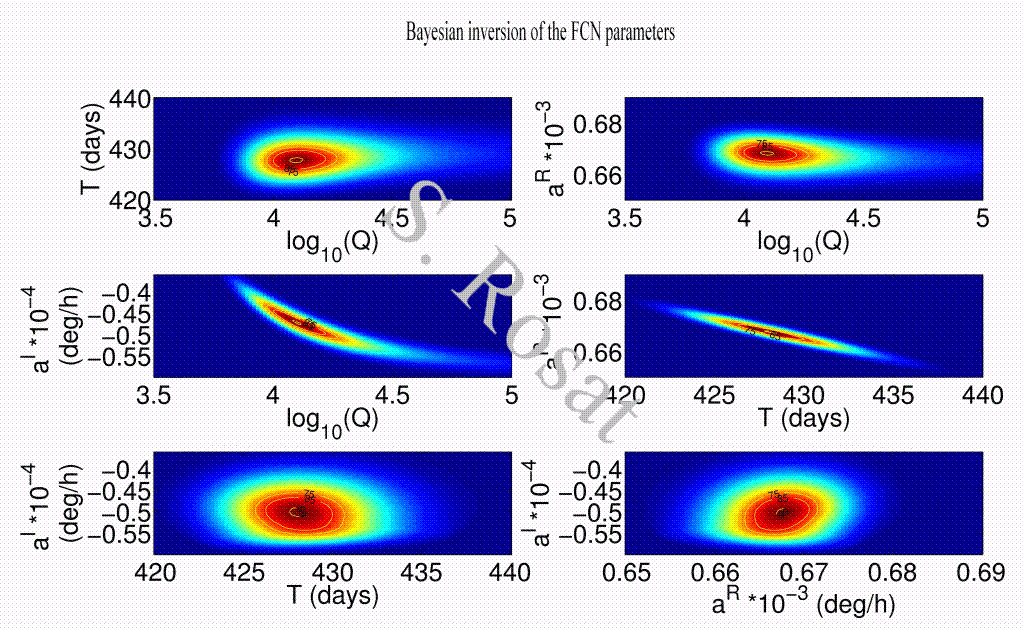
Free Core Nutation Resonance

The Bayesian package for the inversion of the parameters of the FCN resonance is available in the Ressources section.

Free Core Nutation Resonance: Bayesian inversion of the FCN parameters from the combination of 7 SGs gravimetric data
Free Core Nutation Resonance: Bayesian inversion of the FCN parameters from the combination of 7 SGs gravimetric data

Seismic modes

Seismic modes after the 2011 Mw9 Sendai earthquake at Strasbourg (France) Superconducting Gravimeter site
Seismic modes after the 2011 Mw9 Sendai earthquake at Strasbourg (France) Superconducting Gravimeter site
Seismic modes after the 2010 Mw8.8 Chile earthquake at some Superconducting Gravimeter sites
Seismic modes after the 2010 Mw8.8 Chile earthquake at some Superconducting Gravimeter sites
0S2 amplitude spectrum at Strasbourg (France) superconducting gravimeter site after the 2004 Mw9.0 Sumatra-Andaman earthquake
0S2 amplitude spectrum at Strasbourg (France) superconducting gravimeter site after the 2004 Mw9.0 Sumatra-Andaman earthquake
2S1 amplitude spectrum at Strasbourg (France) superconducting gravimeter site after the 2004 Mw9.0 Sumatra-Andaman earthquake
2S1 amplitude spectrum at Strasbourg (France) superconducting gravimeter site after the 2004 Mw9.0 Sumatra-Andaman earthquake
Comparison at Matsushiro (Japan) between the SG and STS1 seismometer records after the 2004 Mw9.0 Sumatra-Andaman earthquake
Comparison at Matsushiro (Japan) between the SG and STS1 seismometer records after the 2004 Mw9.0 Sumatra-Andaman earthquake

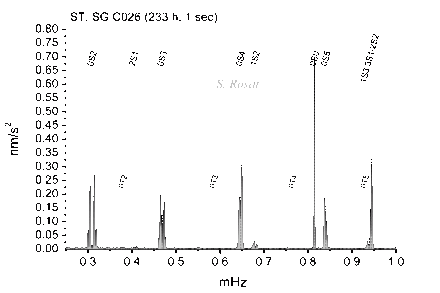
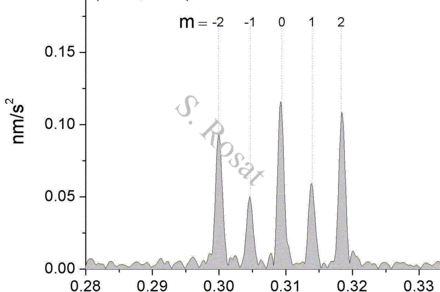
Excitation amplitude of the "Slichter mode"

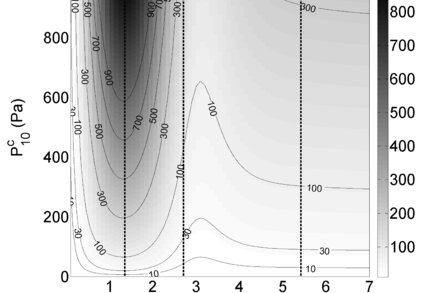
Excitation amplitude of the Slichter mode for a zonal degree-one pressure flow in the core as function of the characteristic time of the source. Theoretical computation for a PREM-like Earth's model using a Green function formalism
Excitation amplitude of the Slichter mode for a zonal degree-one pressure flow in the core as function of the characteristic time of the source. Theoretical computation for a PREM-like Earth's model using a Green function formalism (Rosat & Rogister 2012).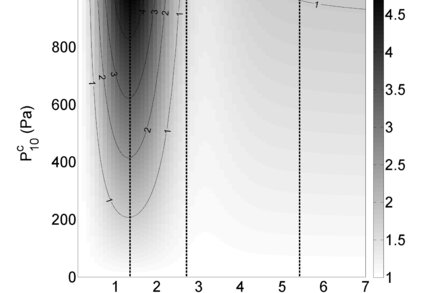
Excitation amplitude of the Slichter mode for a zonal degree-one surface load density as function of the characteristic time of the source. Theoretical computation for a PREM-like Earth's model using a Green function formalism
Excitation amplitude of the Slichter mode for a zonal degree-one surface load density as function of the characteristic time of the source. Theoretical computation for a PREM-like Earth's model using a Green function formalism (Rosat & Rogister 2012).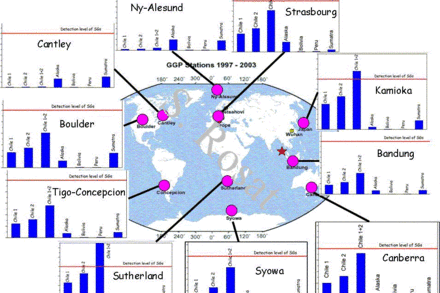
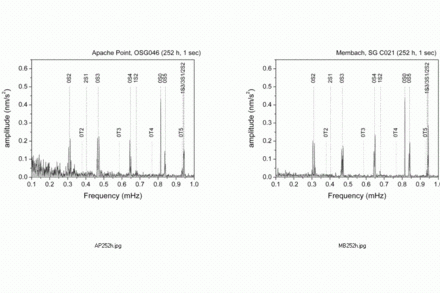
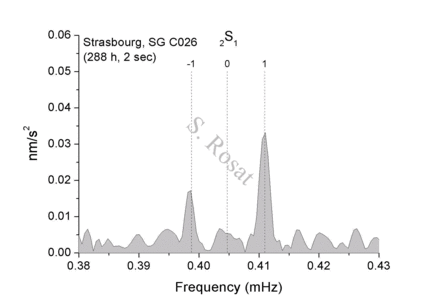
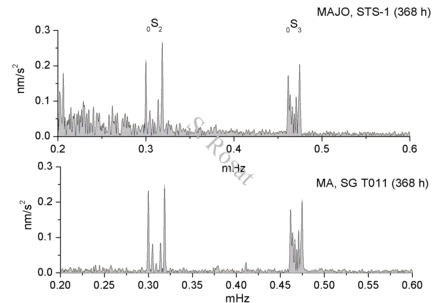
Seismic excitation amplitude of the Slichter mode at SG sites. Theoretical computation for a PREM-like Earth's model using a Green function formalism
Seismic excitation amplitude of the Slichter mode at SG sites. Theoretical computation for a PREM-like Earth's model using a Green function formalism (Rosat 2007, Rosat HdR 2016).

Observed noise and self-noise of a Superconducting Gravimeter vs predicted Slichter mode amplitude

Observed vs self-noise of a Superconducting Gravimeter (iGrav#015) recording at the gravimetric Observatory of Strasbourg
The seismological reference noise model NLNM is plotted in red. Horizontal dashed gray segments represent the levels of detection of harmonic signals of respective amplitudes 0.3 and 1 nGal. The dashed black line is the predicted PSD amplitude for the Slichter mode (1S1) excited by the surface atmospheric ECMWF pressure field (Rosat et al. 2014). The 95 % confidence interval (C.I.) of the PSD estimate is indicated (From Rosat & Hinderer, 2018).

The so-called "Slichter" mode or "Slichter" triplet is a normal mode of the Earth consisting of a translational oscillation of the solid inner-core within the fluid outer core at a period close to 5 hours. The existence of this spheroidal mode, noted 1S1 in seismology, was first suggested by Slichter (1960). This mode raised some controversies in the past associated with its theoretical frequency (related to the value of the density jump at the inner-core boundary), its splitting by rotation and ellipticity (role of the outer core viscosity) and in terms of its detection in gravimetric records. Today, the observation of this mode is still a challenge since its predicted surface amplitude is smaller than other surficial effects and below the level of detection (noise level in terms of Power Spectral Density) of geophysical instruments, by two orders of magnitude with respect to the observed noise level of Superconducting Gravimeters, but less than one order of magnitude with respect to their self-noise (Rosat & Hinderer, 2018).